| Issue |
Radioprotection
Volume 53, Number 4, October-December 2018
|
|
|---|---|---|
| Page(s) | 255 - 263 | |
| DOI | https://doi.org/10.1051/radiopro/2018032 | |
| Published online | 12 November 2018 | |
Article
Natural radioactivity measurements and external dose estimation by car-borne survey in Douala city, Cameroon
1
Nuclear Physics Laboratory, Faculty of Science, University of Yaoundé I,
P.O. Box 812
Yaoundé, Cameroon
2
Nuclear Technology Section, Institute of Geological and Mining Research,
P.O. Box 4110
Yaoundé, Cameroon
3
Hirosaki University Graduate School of Health Sciences,
Hirosaki City,
Aoromi, Japan
4
National Institute for Fusion Science,
322-6 Oroshi,
Toki,
Gifu
509-5292, Japan
5
Department of Radiation Physics, Institute of Radiation Emergency Medicine, Hirosaki University,
Hirosaki City,
Aomori
036-8564, Japan
* Corresponding author: saidous2002@yahoo.fr
Received:
23
January
2018
Accepted:
27
July
2018
A car-borne survey was carried out in Douala, the largest city in Cameroon to make a detailed distribution map of the absorbed dose rate in the city, to locate the high natural radiation areas useful later to carry out indoor radon, thoron, and thoron progeny measurements. Gamma-ray dose rates were measured using 3-in × 3-in NaI(Tl) detector. Activity concentrations of 238U, 232Th and 40K in soil from Douala city were determined by two methods: the first, using in situ gamma spectrometry and the second, at the laboratory using a NaI(Tl) detector. A heterogeneous distribution of absorbed dose rates in air was observed on the dose rate distribution map, and varies from 29 to 86 nGy h−1 with an average of 50 nGy h−1, lower than the world average value of 59 nGy h−1. The activity concentrations with NaI(Tl) detector varied from 18 to 47 Bq kg−1 for 238U, 21 to 54 Bq kg−1 for 232Th, and 10 to 410 Bq kg−1 for 40K with averages of 29, 38, and 202 Bq kg−1 respectively, for in situ measurements. They vary between 29–98 Bq kg−1 for 238U, 29–92 Bq kg−1 for 232Th, and 40 to 79 Bq kg−1 for 40K, with averages of 60, 57, and 56 Bq kg−1 respectively for soil samples collected at Douala III subdivision. The highest value of the annual effective dose for in situ measurements by car was observed at Ndogbong and was found to be 0.7 mSv y−1, higher than the world average value of 0.5 mSv y−1.
Key words: car-borne survey / NaI(Tl) detector / natural radioactivity / air absorbed dose rate / external effective dose
© EDP Sciences 2018
1 Introduction
Exposure to natural radiation sources varies substantially from one area to another and even locally (UNSCEAR, 1982). Gamma radiation from natural radionuclides such as 238U, 232Th and 40K is the main source of external exposure. There are three sources of environmental radioactivity: terrestrial, manmade and cosmic. The most significant terrestrial radionuclides include the uranium and thorium decay series, potassium and rubidium (EPA, 2009). The terrestrial component is due to the radioactive nuclides that are present in air, soil, rocks, water and building materials whose amounts vary significantly depending on the geological and geographical features of the regions. Cosmic radiation from space contributes to the background changes chiefly through elevation and latitude (UNSCEAR, 2000). Although background radiation is present everywhere, radionuclide concentrations and distributions are not constant (EPA, 2009). For ages, humans have been exposed to radionuclides that occur naturally in the environment. It is therefore important to measure the activity concentrations of radionuclides in the living environment.
There have been many surveys to measure natural radioactivity and to estimate corresponding radiation dose to the public in Cameroon. According to Guembou et al. (2017), absorbed dose rates and annual effective dose due to radioactivity in sand used as building material in Douala, were normal and within the recommended limits. Also, Saïdou et al. (2015a, 2015b) reported no significant radiological risk to population living in the oil-bearing Bakassi peninsula, in the uranium-bearing regions of Poli and Lolodorf. The average total radiation dose and external radiation dose were respectively 5.9 and 0.6 mSv y−1 for Poli, 7.6 and 0.7 mSv y−1 for Lolodorf, and 22.3 and 0.3 mSv y−1 for Bakassi.
In this study, a car-borne survey was carried out to establish the dose rate distribution map, to assess the annual external dose and to perform natural radioactivity measurements in soil from Douala, the largest city in Cameroon. Gamma ray spectrometry based on NaI(Tl) detector was also used in the laboratory to determine activity concentrations of 238U, 232Th and 40K in soil.
2 Material and methods
2.1 Survey area
Douala is a coastal city, the economic capital of Cameroon, the main business center and the largest city of the country; with approximately 4 million inhabitants. It is the chief town of the Littoral Region and the Wouri Division. Located on the edge of the Atlantic Ocean, at the bottom of the Gulf of Guinea, at the mouth of the Wouri River, Douala has the largest port in the Cameroon and one of the most important in Central Africa. The annual rainfall ranges between 3000 and 5000 mm, and the annual average temperature is 26 °C (Olivry, 1986). The geology of the region consists of sedimentary rocks, mainly, tertiary and quaternary sediments (Ndontchueng et al., 2014).
2.2 Car-borne survey
A car-borne survey was carried out using a mobile vehicle moving at a speed of approximatively 40 km h−1, in which was positioned a measuring system consisting of a sodium iodide detector 3-in × 3-in NaI(Tl), a global positioning system (GPS) to record coordinates at each measuring point, and a computer to analyze gamma-ray spectra (EMF-211, EMF Japan Co, Japan). Absorbed dose rate measurements inside the vehicle were performed every 30 seconds along the way and corrected by multiplying with a shielding factor with the aim of representing the unshielded external dose rate. The shielding factor (Fig. 1) was evaluated in order to be able to convert the values measured inside the vehicle to ambient dose rate outside of the car, and was estimated by making measurements inside and outside the vehicle at 10 measurement points and correcting them with count rates inside. The absorbed dose rates in air were calculated using a dose rate conversion factor based on the correlation of dose rate (nGy h−1) and total count rate (cpm) from 0 to 1023 channels in the gamma-ray pulse height distribution (Hosoda et al., 2015, 2016). Commonly, the gamma-ray pulse height distribution is obtained by 15 min measurements at each point. Measurements of gamma-ray pulse height distributions were carried out at 1 m above the ground surface at 39 measurement points in Douala City. The gamma-ray pulse height distributions were unfolded using a 22 × 22 response matrix for the estimation of absorbed dose rate in air (Minato and Kawano, 1970; Minato, 2001). The dose rate conversion factor of the scintillation spectrometer used in the present survey was determined to be 1.75 × 10−3 nGy h−1.cpm−1. Figure 2 gives the relationship between absorbed dose rate (nGy h−1) which was calculated by software using the response matrix method and total count rates outside the vehicle. Absorbed dose rate in air (Dout) 1 m above the ground surface at each measurement point can be estimated by the following equation (Tan et al., 2017):
 (1)
where (Din) is the count rate inside the car (cps) obtained by the measurements for 30 seconds. Since the dose rate conversion factor was given as a dose rate (nGy h−1) for counts per minute (cpm), it is necessary to double Din in order to convert into the counts per minute.
(1)
where (Din) is the count rate inside the car (cps) obtained by the measurements for 30 seconds. Since the dose rate conversion factor was given as a dose rate (nGy h−1) for counts per minute (cpm), it is necessary to double Din in order to convert into the counts per minute.
Following in situ measurements, external effective dose in Douala was assessed using the following equation (Inoue et al., 2017):
 (2)
where E is the external effective dose (mSv y−1), Dout is the absorbed dose rate in air (nGy h−1), DCF is the dose conversion factor from the dose rate to the external effective dose for adults (0.748 ± 0.007 Sv Gy−1) (Moriuchi et al., 1990), T is 8766 h, and Qin and Qout are indoor (0.6) and outdoor (0.4) occupancy factor respectively. R (1.11) is the ratio of indoor and outdoor dose rate.
(2)
where E is the external effective dose (mSv y−1), Dout is the absorbed dose rate in air (nGy h−1), DCF is the dose conversion factor from the dose rate to the external effective dose for adults (0.748 ± 0.007 Sv Gy−1) (Moriuchi et al., 1990), T is 8766 h, and Qin and Qout are indoor (0.6) and outdoor (0.4) occupancy factor respectively. R (1.11) is the ratio of indoor and outdoor dose rate.
 |
Fig. 1 Correlation between count rates outside and inside the car. This regression formula was used as the shielding factor of the car body. |
 |
Fig. 2 Correlation between absorbed dose rate in air which was calculated by software using the response matrix method and total count rate observed outside the car. This regression formula was used as the dose rate conversion factor. |
2.3 Activity concentrations of 238U, 232Th and 40K and their contribution to the air absorbed dose rate
The evaluation of activity concentrations and the contribution of 238U, 232Th and 40K to the absorbed dose rate in air were obtained by measuring the spectra of gamma-ray pulse height distributions and using a 22 × 22 response matrix conceived by Minato (1978, 2001). The gamma-ray pulse height distribution obtained by measurements was converted to the energy bin spectrum of incident gamma-ray which is a distribution of gamma-ray flux density to each energy bin. The energy ranges from 0 to 3.2 MeV, energies above 3.2 MeV were not included for evaluation because the maximum value of the gamma-ray energy from natural radionuclides is 2.615 Mev emitted by 208Tl (232Th-series). The gamma-ray lines utilized for natural radionuclides are: 1.464 MeV for 40K, 1.768 MeV and 2.205 MeV for 214Bi (238U-series), and also 2.615 MeV for 208Tl (232Th-series). The 22 × 22 matrix for the 3-in × 3-in NaI(Tl) scintillator for an isotropic field was calculated using the Monte Carlo code, SPHERIX (Matsuda et al., 1982; Minato, 2012). The gamma-ray flux density and dose rate per unit solid angle are considered almost isotropic in the natural environment (Minato, 1971). The calculation of gamma-ray flux densities per unit activity concentrations of 238U-series, 232Th-series and 40K are necessary, in order to evaluate each activity concentrations of natural radionuclides from an energy bin spectrum. This calculation assumed that a semi-infinite volume source was formed in the ground (Minato, 2001). The primary and scattered gamma-ray flux density per unit activity concentrations could be calculated using one-dimensional Monte Carlo gamma transport code, MONARIZA/G2 (Minato, 1977, 1980). A total of a million histories were traced for each natural radionuclide. The nuclear data of gamma-ray energies and disintegration rates used the reported values by Beck (1972) and Beck et al. (1972) for this Monte Carlo simulation. The activity concentration of each natural radionuclide was evaluated by a successive approximation which used a 3 × 3 matrix, determined by Minato (2001), to the values of energy bins for 238U-series, 232Th-series and 40K. The statistical errors for absorbed dose rates in air and activity concentrations for 40K, 238U-series and 232Th-series obtained using this software depend on the integral air kerma (nGy h−1) at each measurement point (Matsuda et al., 2002), and these were evaluated in this study as 2%, 2%, 6–8% and 4–5%, respectively.
2.4 Sampling and sample preparation
For radioactivity measurements in soil, twenty soil samples from a depth of 0–5 cm, weighing about 1 kg each were collected at Douala III, pulverized and then dried at a temperature of 70 °C for 48 hours to remove moisture. Samples were then transferred to Marinelli containers of 500 cm3, each hermetically sealed and stored for more than 40 days to bring 222Rn and its short-lived daughter products into equilibrium with 226Ra (Ravisankar et al., 2011).
2.5 Radioactivity measurements in laboratory
238U, 232Th and 40K activity concentrations in soil samples were measured using a gamma ray spectrometer. The samples were placed in a shielded gamma ray spectrometry unit for a counting time of 105 seconds. Radioactivity measurements were carried out using a NaI(Tl) detector of 7.6 cm × 7.6 cm size and a resolution of 7.5% at 661.6 keV with a 1024 channels multichannel analyzer. The detector was calibrated using the standard gamma ray source of 137Cs with known peak at 661.6 keV, 152Eu with known peaks at 1089.7 keV, and 1408.1 keV and 60Co with known peaks at 1173.2 keV and 1332.5 keV. The efficiency calibration curve for NaI(Tl) detector was obtained using standards containing 40K (1460.8 keV), 137Cs (661.6 keV), 208Tl (2614.4 keV) and 228Ac (940.1 keV). Gamma-ray lines of 214Bi were used to determine 238U activity concentrations after reaching secular equilibrium between 222Rn and its daughter products 214Bi and 214Pb. Gamma-ray lines of 228Ac were considered to determine activity concentrations of 232Th.
The spectral analysis was performed using Genie-2000. Activity concentrations of natural radionuclides in samples were computed using the following equation (IAEA, 1989):
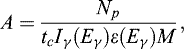 (3)
where NP is the number of counts in a given peak area corrected for background peaks of a peak at energy E, ϵ(Eγ) the detection efficiency at energy E, tc is the counting lifetime, Iγ(Eγ) is the number of gamma rays per disintegration of this nuclide at energy E, and M the mass in kg of the sample.
(3)
where NP is the number of counts in a given peak area corrected for background peaks of a peak at energy E, ϵ(Eγ) the detection efficiency at energy E, tc is the counting lifetime, Iγ(Eγ) is the number of gamma rays per disintegration of this nuclide at energy E, and M the mass in kg of the sample.
2.6 Estimation of absorbed dose rate in air and external effective dose
The external terrestrial gamma-radiation absorbed dose rates in air at a height of about 1 m above the ground are calculated by using the conversion factor 0.0417 (nGy h−1)(Bq kg−1)−1 for 40K, 0.462 (nGy h−1)(Bq kg−1)−1 for 238U and 0.604 (nGy h−1)(Bq kg−1)−1 for 232Th (UNSCEAR, 2000). Assuming that, 137Cs, 90Sr and the 235U decay series can be neglected as they contribute very little to the total dose from the environmental background (Kocher and Sjoreen, 1985; Jacob et al., 1986; Leung et al., 1990):
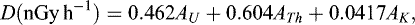 (4)
where AU, ATH and AK are the mean activity concentrations of 238U, 232Th and 40K, respectively in (Bq kg−1).
(4)
where AU, ATH and AK are the mean activity concentrations of 238U, 232Th and 40K, respectively in (Bq kg−1).
In the estimation of external effective dose, the conversion coefficient and occupancy factor must be taken into account. In the present work, a conversion factor of 0.7 Sv Gy−1 and occupancy factors Q have been used to convert the absorbed rate to human effective dose equivalent with an outdoor and indoor occupancy of 40% and 60% respectively. However, since the materials used in the construction of most these buildings also contain radionuclides, R (1.11) is the ratio of indoor and outdoor dose rate (Fig. 3). It should be noted that the dwellings were built mainly using locally made soil bricks. Ai are average activity concentrations of 238U, 232Th and 40K. (KCF)i are corresponding air kerma conversion factors given previously. The external effective dose is determined as follows (Saïdou et al., 2015b):
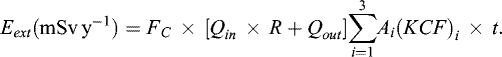 (5)
(5)
 |
Fig. 3 Correlation between outdoor and indoor dose obtained by car-borne survey in Douala rate. |
3 Results and discussion
3.1 Shielding factor and dose rate conversion factor
The relationship between count rates inside and outside the car is shown in Figure 1, and the shielding factor and standard uncertainty (JCGM 100, 2008) were found to be 1.62 and 0.03, respectively. However, the shielding factor is influenced by the type of car, number of passengers and detector position inside the car.
Figure 2 shows the correlation between absorbed dose rates in air (nGy h−1) calculated using the 22 × 22 response matrix method and count rate outside the car (cps) (that is corrected count rate inside the car). The dose conversion factor and uncertainty were found to be 0.00175 nGy h−1 cps−1 and 0.01, respectively (Fig. 2). Thus, the absorbed dose rate in air (Dout) outside the car 1 m above the ground surface at each measuring point can be estimated using the following equation (Tan et al., 2017):
 (6)
where (Din) is count rate inside the car (cps) obtained by measurements for 30 seconds.
(6)
where (Din) is count rate inside the car (cps) obtained by measurements for 30 seconds.
3.2 Air absorbed dose rate distribution in Douala city and effective external dose
Figure 4 shows the survey route and Figures 5 and 6 show the measurement points of gamma-ray pulse height distribution of Douala. The highest air absorbed dose rates (86 nGy h−1) were observed at Ndogbong (N4.058778, E9.74635). The absorbed dose rates in this study range between 28–86 nGy h−1 with the average value of 50 nGy h−1 (Fig. 7). According to UNSCEAR (2000) at worldwide level, gamma dose rates in air range between 24–160 nGy h−1 and the average is 59 nGy h−1, higher than the average value obtained within the framework of this study. However at Ndogbong, Aeroport, Ndogpassi III, Bepanda Omnisports, and Brazzaville, air absorbed dose rates are higher than the worldwide average value. The town of Kerala in India recorded large values of the absorbed dose rate, up to 2100 nGy h−1, observed near the rare earth mining (Hosoda et al., 2015). In Tokyo, air absorbed dose rates range from 18 to 76 nGy h−1 with an average value of 49 nGy h−1 (Inoue et al., 2015), and from 9 to 554 nGy h−1 with an average value of 50 nGy h−1 in Turkey (Turhan et al., 2012), which is practically lower than the corresponding worldwide value.
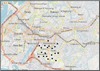 |
Fig. 4 Survey route in Douala. This map was also drawn using QGIS (Background: Openstreet map). |
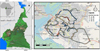 |
Fig. 5 Location of sampling point (20) pulse. |
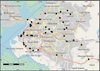 |
Fig. 6 In situ measurement points (39) of gamma-ray pulse height distribution using a NaI(Tl) scintillation spectrometer. |
 |
Fig. 7 Histogram of absorbed dose rate in air. |
3.3 Effective dose assessment
The external annual effective dose ranged from 0.21 to 0.41 mSv y−1 with a mean value of 0.31 mSv y−1, less than the worldwide average value of 0.5 mSv y−1 (UNSCEAR, 2000). In the Gold Mining Areas of Betare-Oya, Eastern-Cameroon, the mean value of effective dose is 0.33 mSv y−1 (0.17–0.60 mSv y−1) (Ngoa et al., 2017) and in Tokyo, before the Fukushima Daiichi Nuclear Power plant Accident, the arithmetic annual effective dose was 0.32 mSv y−1 (0.26–0.40 mSv y−1) (Inoue et al., 2015), which are practically lower than the corresponding worldwide value.
3.4 In situ activity concentrations of 238U, 232Th and 40K and their contribution to air absorbed dose rate
According to Table 1, activity concentrations for primordial radionuclides range between 18–47 Bq kg−1, 21–54 Bq kg−1 and 110–410 Bq kg−1 for the 238U series, 232Th series and 40K respectively, with corresponding average values of 29 Bq kg−1, 38 Bq kg−1 and 202 Bq kg−1. For 238U and 232Th, 7/39 and 32/39 measurement points have respectively activity concentrations higher than the world average value (UNSCEAR, 2000). For 40K, 1/39 measurement point has activity concentrations higher than the world average. By comparing the average in situ activity concentrations of 238U, 232Th and 40K in Douala with the average values in other areas of Cameroon and other countries as shown in Table 3, it should be noted that the mean activity concentration of 238U is higher than the average value measured in other areas of Cameroon such as Bakassi and Poli, and lower than those measured in Lolodorf and Douala quarries. The same comparison can be made with those measured in Lagos state in Nigeria, in Itagunmodi and Canakkale in Turkey, and in Kerala in India. For 232Th, the average activity concentration found out in the present study is higher than those of Bakassi and Poli, and lower than those measured at Douala-quarriers and Lolodorf. This value is also higher than those of Itagunmodi and Lagos State and lower than that of Kerala. The average value of 40K is higher than that is obtained in Bakassi and less than the average values found at Douala-quarriers, Lolodorf and Poli. Compared to other studies in the world, this value is higher than that of Canakkale, lower than those of Lagos state, Itagunmodi and Kerala. Figure 8 shows a weak correlation between thorium and uranium (correlation coefficient = 0.09).
The contributions of 238U, 232Th and 40K to the absorbed dose rates in air range respectively between 21–44%, 36–61% and 12–36% with the average values of 27%, 54% and 19% respectively. The highest contributions of 238U, 232Th and 40K to the absorbed dose rate were respectively found at Akwa (44%) (N4.04285, E9.705237), Beedi (61%) (N4.053658, E9.761817) and SCDP (36%) (N4.06649, E9.703935) while the lowest contributions were found at Makepe (36%) (N4.04285, E9.705237) and Akwa (12%) (N4.017505, E9.715673) for 232Th and 40K respectively.
In situ activity concentrations and the contributions of 40K, 238U and 232Th to air absorbed dose rates in Douala using the car-borne survey method.
 |
Fig. 8 Correlation between 232Th and 238U activity concentrations. |
3.5 Activity concentrations of 238U, 232Th and 40K in soil following laboratory measurements
Activity concentrations of natural radionuclides 238U, 232Th and 40K in 20 soil samples using gamma spectrometry in laboratory are listed in Table 2. They range respectively between 29–96 Bq kg−1, 29–92 Bq kg−1, and 40–79 Bq kg−1 with respective average values of 60 Bq kg−1, 57 Bq kg−1 and 56 Bq kg−1. The world average values of 238U, 232Th and 40K in the earth’s crust are 35, 30 and 400 Bq kg−1, respectively (UNSCEAR, 2000). It appears that average values of 238U and 232Th are higher than the corresponding world average activity concentrations. Figure 9 shows a good correlation between thorium and uranium in soil samples (correlation coefficient = 0.97). The highest 238U and 232Th activity concentrations were found at Brazzaville (96 Bq kg−1), and Dakar for 40K (79 Bq kg−1) and the lowest activity concentrations of 238U and 232Th were found at Bilongue (29 Bq kg−1) and Oyack for 40K (40 Bq kg−1). The results of activity concentrations of natural radionuclides in soil samples taken from Douala III at different locations and in other parts of the world are displayed in Table 3. It clearly appears that activity concentrations of 238U and 232Th were higher than those of other areas in Cameroon (Bakassi, Poli and Douala-quarries), except Lolodorf and other countries (Lagos state, Itagunmodi, Canakkale).
The external terrestrial gamma radiation absorbed dose rates range between 34 and 102 nGy h−1, with an average value of 65 nGy h−1, which is higher than the world average value of 59 nGy h−1 (UNSCEAR, 2000). According to Table 2, absorbed dose rates at 13 over 20 measurement points were higher than the world average value (59 nGy h−1). External effective dose of 8 over 20 measurement points is higher than the worldwide average value. The highest effective dose was found at Brazzaville (0.7 mSv y−1) and Oyack (0.6 mSv y−1). However, for in situ measurements, Table 1 shows that all measurement points have absorbed dose rate lower than the worldwide average value. External effective dose varies from 0.3–0.7 mSv y−1 with an average value of 0.42 mSv y−1, which is lower than the worldwide average value (0.5 mSv y−1). The average value of the effective amount obtained in this study compared to other inhabited areas of Cameroun (Poli and Lolordorf) is low, and high in Bakassi Saïdou et al., (2015b).
Activity concentrations of 238U, 232Th and 40K in soil, air absorbed dose rates and annual effective dose following radioactivity measurements at the laboratory.
 |
Fig. 9 Correlation between 232Th and 238U activity concentrations. |
Comparison of activity concentrations of 238U, 232Th and 40K in soil samples from Douala littoral region following laboratory and in situ measurements with values from other areas around the world.
4 Conclusion
The car-borne survey using NaI(Tl) scintillation spectrometer was carried out in Douala, the largest city of Cameroon to make the detailed distribution map of absorbed dose rate in air. Activity concentrations of 238U, 232Th and 40K were also determined using in situ gamma spectrometry. They range respectively between 18–47 Bq kg−1, 21–54 Bq kg−1 and 110–410 Bq kg−1 with respective average values of 29 Bq kg−1, 38 Bq kg−1 and 202 Bq kg−1. Mean activity concentrations of 238U and 40K are lower than the world average values (UNSCEAR, 2000) while the mean activity concentration of 232Th is higher than the corresponding world average value. The contributions of 238U, 232Th and 40K to the absorbed dose rates in air range respectively between 21–44%, 36–61% and 12–36% with the average values of 27%, 54% and 19%. The average activity concentrations of natural radionuclides 238U, 232Th and 40K in the soil were found to be 60 Bq kg−1, 57 Bq kg−1 and 56 Bq kg−1 respectively. The total average effective dose is 0.37 mSv y−1 which is lower than the worldwide average value (0.5 mSv y−1). Finally, it can be concluded that the population of Douala city is not significantly exposed to natural radiation.
References
- Ademola KA, Bello KA, Adejumobi CA. 2014. Determination of natural radioactivity and hazard in soil samples in and around gold mining area in Itagunmodi, south-western, Nigeria. J. Radiat. Res. Appl. Sci. 7: 249–255. [Google Scholar]
- Beck HL. 1972. The absolute intensities of gamma rays from the decay of 238U and 232Th. Health and Safety Laboratory Report HASL-262. New York: U.S. Atomic Energy Commission. [Google Scholar]
- Beck HL, DeCampo J, Gogolak C. 1972. In-situ Ge(Li) and NaI(T1) gamma-ray spectrometry. Health and Safety Laboratory Report HASL-258. New York: U.S. Atomic Energy Commission. [Google Scholar]
- EPA. 2009. Sources of background radioactivity. http://www.epa.gov/radiation/marssim/docs/marsame/appendix.B.pdf. Accessed 9 August 2011. [Google Scholar]
- Guembou Shouop SJ, Ndontchueng Moyo M, Chene G, Nguelem Mekontso EJ, Motapon Ousmanou, Kayo AS, Strivay D. 2017. Assessment of natural radioactivity and associated radiation hazards in sand building material used in Douala Littoral Region of Cameroon using gamma spectrometry. Environ. Earth Sci. 76: 1–12. [Google Scholar]
- Hosoda M, Tokonami S, Omori Y, Sahoo SK, Akiba S, Sorimachi A, Ishikawa T, Nair RR, Jayalekshmi PA, Sebastian P, Iwaoka K, Akata N, Kudo H. 2015. Estimation of external dose by car-borne survey in Kerala, India. Plos ONE 10: e0124433. [Google Scholar]
- Hosoda M, Inoue K, Oka M, Omori Y, Iwaoka K, Tokonami S. 2016. Environmental radiation monitoring and external dose estimation in Aomori prefecture after the Fukushima Daiichi Nuclear Power Plant accident. Jpn. J. Health Phys. 51: 41–50. [CrossRef] [Google Scholar]
- IAEA. 1989. Measurement of radionuclides in food and the environment, a guidebook. International Atomic Energy Agency Technical Reports Series No. 229, Vienna. [Google Scholar]
- Inoue K, Hosoda M, Fukushi M, Furukawa M, Tokonami S. 2015. Absorbed dose rate in air in metropolitan Tokyo before the Fukushima Daiichi Nuclear Power Plant accident. Radiat. Prot. Dosim.167: 231–234. [Google Scholar]
- Inoue K, Arai M, Fujisawa M, Saito K, Fukushi M. 2017. Detailed distribution map of absorbed dose rate in air in Tokatsu area of Chiba prefecture, Japan, constructed by car-borne survey 4 years after the Fukushima Daiichi Nuclear Power Plant accident. Plos ONE 12: e0171100. [CrossRef] [PubMed] [Google Scholar]
- Jacob P, Paretzke HG, Rosenbaum H, Zankl M. 1986. Effective dose equivalents for photon exposure from plane sources on the ground. Radiat. Prot. Dosim. 14: 299–310. [Google Scholar]
- JCGM 100. 2008. Joint Committee for Guides in Metrology. Evaluation of measurement data-guide to the expression of uncertainty in measurement, September 2008. http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf. Accessed 19 August 2016. [Google Scholar]
- Kocher DC, Sjoreen AL. 1985. Dose-rate conversion factors for external exposure to photon emitters in soil. Health Phys. 48: 193–205. [CrossRef] [PubMed] [Google Scholar]
- Leung KC, Lau SY, Poon CB. 1990. Gamma radiation dose from radionuclides in Hong Kong soil. J. Environ. Radioact. 11: 279–290. [Google Scholar]
- Matsuda H, Furukawa S, Kaminishi T, Minato S. 1982. A new method for evaluating weak leakage gamma-ray dose using a 3”φ × 3” NaI(Tl) scintillation spectrometer (I) Principle of background estimation method. Rep Government Industrial Research Institute. Nagoya 31: 132–146. In Japanese. [Google Scholar]
- Matsuda H, Minato S, Pasquale V. 2002. Evaluation of accuracy of response matrix method for environmental gamma ray analysis. Radioisotopes 51: 42–50. In Japanese. [Google Scholar]
- Minato S. 1971. Terrestrial gamma-radiation field in natural environment. J. Nucl. Sci. Technol. 8: 342–347. [Google Scholar]
- Minato S. 1977. Analysis of the variation of environmental γ radiation during rainfall. Rep Government Industrial Research Institute. Nagoya 26: 190–202. In Japanese. [Google Scholar]
- Minato S. 1978. A response matrix of a 3”φ × 3” NaI(Tl) scintillator for environmental gamma radiation analysis. Rep Governmental Industrial Research Institute. Nagoya 27: 384–397. In Japanese. [Google Scholar]
- Minato S. 1980. Monte Carlo calculation of gamma radiation field due to precipitation washout of radon daughters from the atmosphere to the ground surface. Jpn. J. Health Phys. 15: 19–24. [CrossRef] [Google Scholar]
- Minato S. 2001. Diagonal elements fitting technique to improve response matrixes for environmental gamma ray spectrum unfolding. Radioisotopes 50: 463–471. [Google Scholar]
- Minato S. 2012. Application of a 60 × 60 response matrix for a NaI(Tl) Scintillator to fallout from the Fukushima reactor accident. Radiat. Emerg. Med. 1: 108–112. [Google Scholar]
- Minato S, Kawano M. 1970. Evaluation of exposure due to terrestrial gamma-radiation by response matrix method. J. Nucl. Sci. Technol. 7: 401–406. [Google Scholar]
- Moriuchi S, Tsutsumi M, Saito K. 1990. Examination on conversion factors to estimate effective dose equivalent from absorbed dose in air for natural gamma radiations. Jpn. J. Health Phys. 25: 121–128. Japanese with English abstract. [Google Scholar]
- Ndontchueng MM, Njinga RL, Nguelem EJM, Simo A, Beyala Ateba JF. 2014. 238U, 235U, 137Cs and 133Xe in soils from two campuses in University of Douala-Cameroon. Appl. Radiat. Isot. 86: 85–89. [Google Scholar]
- Ngoa EL, Ndjana NJE, Hosoda M, Bongue D, Saïdou, Akata N, Koukong HR, Kwato NMG, Tokonami S. 2017. Air absorbed dose rate measurements and external dose assessment by car-borne survey in the gold mining areas of Betare-Oya, Eastern-Cameroon. Jpn. J. Health Phys. 53: 5–11. [Google Scholar]
- Ojo TJ, Gbadegesin KAJ. 2015. Terrestrial radiation doses from selected towns of Southwestern Nigeria. Int. J. Phys. 3: 244–247. [Google Scholar]
- Olivry CJ. 1986. Fleuves et rivières du Cameroun. Collection Monographies Hydrologiques. Paris : ORSTOM, no 9. [Google Scholar]
- Ravisankar R, Vanasundari K, Chandrasekaran A, Suganya M, Eswaran P, Vijayagopal P, Meenakshisundaram V. 2011. Measurement of natural radioactivity in brick samples of Namakkal, Tamilnadu, India using gamma ray spectrometry. Arch. Phys. Res. 2: 95–99. [Google Scholar]
- Saïdou, Abdourahimi, Tchuente Siaka YF, Kwato Njock MG. 2015a. Natural radiation exposure to the public in the oil bearing Bakassi Peninsula, Cameroon. Radioprotection 50(1): 35–41. [Google Scholar]
- Saïdou, Ele Abiama P, Tokonami S. 2015b. Comparative study of natural radiation exposure to the public in three uranium and oil regions of Cameroon. Radioprotection 50(4): 265–271. [Google Scholar]
- Tan VL, Inoue K, Fujisawa M, Arai M, Fukushi M. 2017. Impact on absorbed dose rate in air from Asphalt Pavement Associated with Transport Infrastructure Developments on Phu Quoc Island, Vietnam. Radiat. Environ. Med. 2: 88–93. [Google Scholar]
- Turhan S, Arıkan IH, Oğuz F, Ӧzdemir T, Yücel B, Varinlioğlu A, Köse A. 2012. Car-borne survey of natural background gamma dose rate in Çanakkale region, Turkey. Radiat. Prot. Dosim. 148: 45–50. [Google Scholar]
- UNSCEAR. 1982. Ionizing radiation sources and biological effects. United Nations, New York. [Google Scholar]
- UNSCEAR. 2000. Report to the general assembly, with scientific annexes. Annex B exposures from natural radiation sources. New York Report of the United Nations Scientific. [Google Scholar]
Cite this article as: Takoukam Soh SD, Saïdou, Hosoda M, Ndjana Nkoulou II JE, Akata N, Bouba O, Tokonami S. 2018. Natural radioactivity measurements and external dose estimation by car-borne survey in Douala city, Cameroon. Radioprotection 53(4): 255–263
All Tables
In situ activity concentrations and the contributions of 40K, 238U and 232Th to air absorbed dose rates in Douala using the car-borne survey method.
Activity concentrations of 238U, 232Th and 40K in soil, air absorbed dose rates and annual effective dose following radioactivity measurements at the laboratory.
Comparison of activity concentrations of 238U, 232Th and 40K in soil samples from Douala littoral region following laboratory and in situ measurements with values from other areas around the world.
All Figures
 |
Fig. 1 Correlation between count rates outside and inside the car. This regression formula was used as the shielding factor of the car body. |
| In the text | |
 |
Fig. 2 Correlation between absorbed dose rate in air which was calculated by software using the response matrix method and total count rate observed outside the car. This regression formula was used as the dose rate conversion factor. |
| In the text | |
 |
Fig. 3 Correlation between outdoor and indoor dose obtained by car-borne survey in Douala rate. |
| In the text | |
 |
Fig. 4 Survey route in Douala. This map was also drawn using QGIS (Background: Openstreet map). |
| In the text | |
 |
Fig. 5 Location of sampling point (20) pulse. |
| In the text | |
 |
Fig. 6 In situ measurement points (39) of gamma-ray pulse height distribution using a NaI(Tl) scintillation spectrometer. |
| In the text | |
 |
Fig. 7 Histogram of absorbed dose rate in air. |
| In the text | |
 |
Fig. 8 Correlation between 232Th and 238U activity concentrations. |
| In the text | |
 |
Fig. 9 Correlation between 232Th and 238U activity concentrations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




